Consumet: Constructor of surrogate models and metamodels

Consumet is a program which allows the fitting of reduced order models/surrogate models/meta models. But what exactly are these surrogate models, what are their applications, and how can Consumet be useful for your own research? The following blog article tries to answer these questions. In a first step, let us talk a bit about modelling in general.

• Authors: Julian Straus, Jabir Ali Ouassou, and Rahul Anantharaman

Consumet was developed by SINTEF Energy Research as part of the European collaboration ELEGANCY. Click here to download Consumet.

What is a model?

A model is a mathematical representation of a real-world phenomenon. The models can range from the simple to complex depending on the number of  relevant details that are represented in the model.

Detailed, realistic models of chemical processes or physical phenomena are often complex and require a lot of computing power. This is usually acceptable when the model needs to be evaluated once. But, for applications where the model must be evaluated multiple times to identify the “best” solution, such as in an optimisation problem, it is not practical. Instead, simple models are used.

However, it’s often useful to combine accurate predictions of these detailed models in routines like optimization that require mutiple evaluations. The reason is that the used simple models often do not include all relevant phenomena. Hence, the predictions of the simple models are not accurate enough. For example, in the ELEGANCY project, we want to include detailed knowledge about a hydrogen production factory into an investment tool, which would use this information to decide where to place these factories in Norway. The advantage of using the knowledge are more realistic cost estimates and mass balances, and hence, improved results.

• This blog-post might also be of interest: A framework for interdisciplinary collaboration and evaluation of infrastructure transformation in Germany

Simplifying the model maze with Consumet

As it may not be feasible to embed the full realistic model directly into investment tool, we introduce surrogate models. These surrogate models are calculated using the tool Consumet.

Surrogate models are models where the outputs from the detailed model are linked to the model inputs where the link is developed using statistical principles. Thus, surrogate models are simple(r) models with “knowledge” of the detailed models.

We can extract knowledge from a detailed model by systematically varying the input to the model and calculating the corresponding output from the model, a procedure which is called sampling. We then design a simpler kind of model, for example a polynomial function, which we try to fit to the data we sampled.

The result is variously called a reduced-order model because it’s simpler than the original model, a surrogate model because it can be used as a surrogate for the original model, or a metamodel because we have essentially constructed a model of a model.

In any case, this simplified model should be able to produce similar predictions as the original detailed model. But, it requires much less computation time since we do not perform all the physical or chemical calculations. Although such surrogate models are never able to represent the detailed model with 100 % accuracy, we generally aim for a high accuracy.

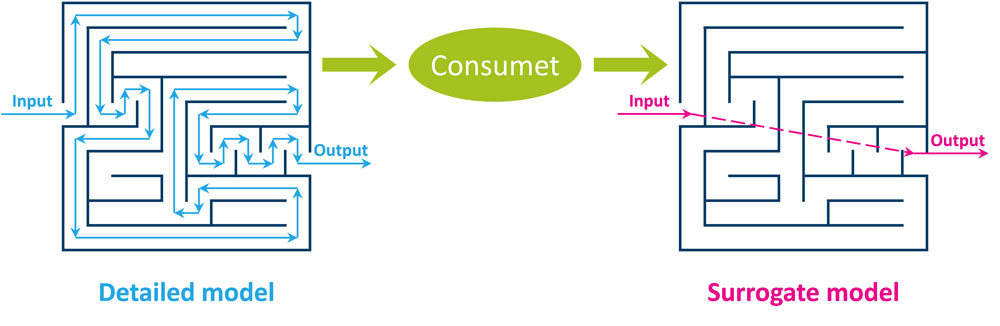
Unfortunately, there is another problem with surrogate models besides the accuracy. They require sampled data from the detailed model. And to obtain this data, it is necessary to evaluate the computationally intensive realistic model over and over again.

In general, the more points we sample, the better the accuracy of the surrogate model. Consumet tries to reduce the required number of sampling points while maintaining or improving the accuracy by a) applying a so-called error-maximization sampling and b) reducing the range of the input variables with the help of user-specified data about the process.

Error-maximization sampling is a so-called adaptive sampling approach. We do not specify values for the input variables one would like to simulate in this approach. Instead, we fit a surrogate model and try to identify input values at which the error between the detailed and surrogate model is highest. This is conducted through an optimization procedure. The main idea is to include these points when updating the model so that both the error in the fitted model and the number of sampling points are reduced.

• This blog-post might also be of interest: ELEGANCY Dutch Case Study: TNO initiates industrial participation with H-Vision project

Limiting the recipe

The input variables range can be reduced through restricting how we vary the input variables. This is perhaps easiest understood via an everyday example: the recipe for a vegetable soup.

On some days, you may prefer to add more potatoes to the soup, while you on other days prefer to add more carrots. However, how much you should add of each ingredient clearly depends on how many people you’re cooking for – so the amounts of potatoes and carrots are both proportional to the total amount of soup. Similarly, you would rarely add extra potatoes and extra carrots to the soup on the same day, so these amounts are inversely proportional to each other. Thus, it would be unwise to independently make decisions for how much soup to cook and how many potatoes or carrots to use.

Chemical processes are quite similar: to find the optimal way to e.g. produce hydrogen, we do not vary the parameters of a chemical plant individually but consider all the relationships between them. Unfortunately, it is not possible to utilize simple procedures as varying a ratio for all cases. Instead, Consumet calculates boundaries for the sampling domain based on provided data. This data must be obtained from parts of the process which are located before the detailed model. Aside of reducing the input range and thus the required computation time, it can in some cases also result in a simpler regression model, which in turn results in a smaller error of the surrogate model.

When to use Consumet

What is then the application of surrogate models, and how can you use them? The answer is quite simple: every time you want to include a detailed model (or its knowledge) into another program for which it is too slow, you should use a surrogate model. This may include optimization of processes, value chain analysis, investment decision tools and many more.

Within ELEGANCY, the aim in the application of surrogate models are in both an investment decision chain tool and a dynamic operational tool of an integrated H₂-CCS chain. Here, surrogate models yield more accurate results, as we can include more detailed knowledge of the physics and chemistry directly in the chain tool.

Consumet can be found on GitHub and is released as open-source software under the terms of the MIT license. It is programmed in Python 3 and utilizes the Pyomo optimization framework for the regression, and the NOMAD optimizer for the error-maximization sampling. The GitHub site also includes a user manual, which describes in detail how to install and use our surrogate modelling tool.