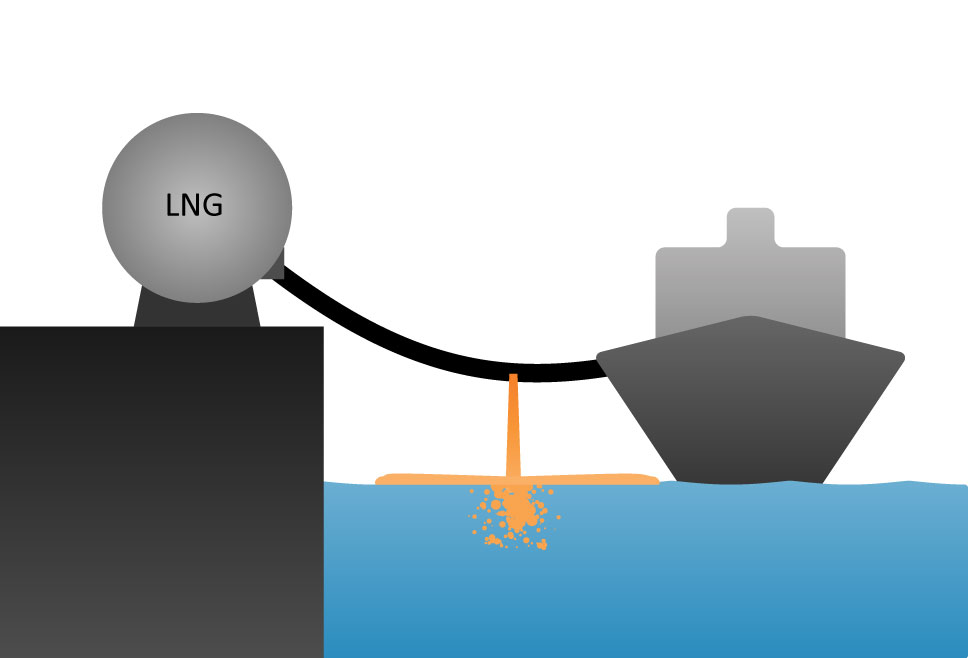
An LNG spill on water may lead to a rapid phase transition (RPT), where overheating of LNG can cause spontaneous evaporation. This can be observed as a type of physical explosion, which may cause damage both to equipment and personnel. We have previously blogged about why LNG Rapid Phase Transitions occur and about using thermodynamics to predict risk and consequence of LNG RPT. Although RPT is a thermodynamic phenomenon, it is strongly dependent on how the LNG and water interact. This is a fluid dynamics problem and so it’s crucial to be able to properly predict how LNG spreads on top of water.
Building on centuries of research on liquid-on-liquid spreading, e.g. LNG spills
As part of the research project ”Predict-RPT” at SINTEF Energy Research, we have worked on how to model the spreading of one liquid on top of another liquid. This important phenomenon has been an active field of study since at least 1774, when Franklin, Brownrigg, and Farish investigated how oil spreads on water and how this can be used to still waves. Our main motivation is to predict how spills of very cold liquids such as liquefied natural gas (LNG) spread on water.
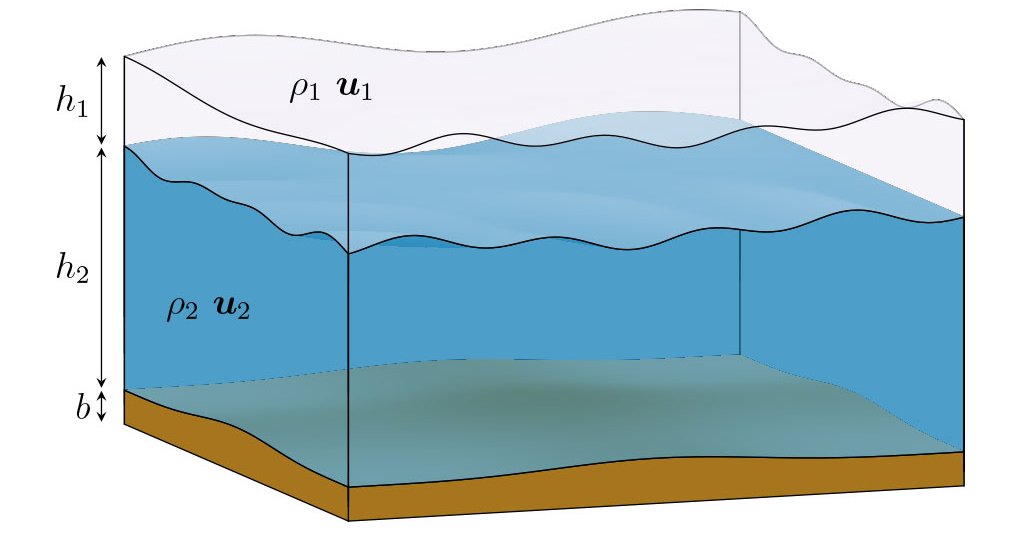
Early on, we soon realised that a set of equations called the shallow-water equations (SWE) (less commonly known as the Saint-Venant equations) would be a good starting point for predicting the spreading of LNG. However, we also found that the standard versions of these equations were not directly suitable. In particular, a liquid spreading on top of another liquid is better modelled by the more complicated two-layer SWE. These equations model both the bottom and the top liquid. Still, in many cases it is a relatively safe assumption that the LNG and water layers are in a buoyant equilibrium, and so it should be possible to simplify and use the standard single-layer SWE. The common approach in the literature is to apply extra conditions on the leading front of the spreading liquid to ensure it is spreading with the right velocity.
Advanced mathematical analysis for accurate predictions
In 2017, we hired a summer intern, Eirik Holm Fyhn, who worked with this problem. That summer we started a two-year long collaboration where Eirik was able to apply advanced mathematical analysis to the SWE. He derived a simple variant of the SWE from the more general two-layer SWE. He mathematically proved that this new variant is a very good approximation to the two-layer SWE where one does not need to apply any extra conditions to the leading edge front. That is, the front velocity is captured directly by the equations. In the common approach, one has to specify this velocity through some semi-empiric closure.
Today, through supervision and collaboration between Eirik and researchers at SINTEF, our paper on this research has been published in in the well-known journal Physics of Fluids. In the paper, we show in a comparison with experiments that our proposed variant of the SWE may be used to accurately predict the spreading of both oil and methane on water.
Useful results in more ways than one
The main result from this work is not only useful to us at SINTEF for predicting the spreading of LNG on water. The results are of general interest and can be used to study a wide range of interesting situations, such as rivers flowing onto water, oil spills on windy oceans, and spills of liquid CO2 or hydrogen.
The results are also interesting from a mathematical perspective. The SWE are hyperbolic conservation laws, and the study of such equations is today a vibrant field of research, for instance at the Toppforsk project WaNP at NTNU. There are still plenty of unsolved problems regarding hyperbolic conservations laws, especially if they form a coupled set of equations or are defined in multiple equations, which is the case for the SWE. It is therefore important to better understand these equations in order to better understand the field of hyperbolic conservation laws. One example of an unsolved problem in this area is to prove the existence and smoothness of the Navier-Stokes equations, which is one of the famous Millenium Prize Problems. The SWE, while looking relatively innocent, is in other words still shrouded in mystery. Our result regarding the intimate connection between the one-layer SWE and the two-layer SWE is one more step in the quest to better understand these equations.
Acknowledgements and academic source: This blog is based on the recent academic paper “A consistent reduction of the two-layer shallow-water equations to an accurate one-layer spreading model” published in Physics of Fluids. This publication is based on results from the research project “Predicting the risk of rapid phase-transition events in LNG spills (Predict-RPT)”, performed under the MAROFF program. The authors acknowledge the Research Council of Norway (244076/O80) for support.
Related blog posts at #SINTEFblog
- 2019-05-06, Svend Tollak Munkejord, ”Film boiling and rapid phase transition of liquefied natural gas”
- 2018-08-14, Eskil Aursand, Morten Hammer, Karl Yngve Lervåg, Gunhild Reigstad, ”Why LNG Rapid Phase Transitions occur (And 3 reasons why they deserve attention)”
- 2018-08-14, Eskil Aursand, Morten Hammer, Karl Yngve Lervåg, Gunhild Reigstad, ”Using thermodynamics to predict risk and consequence of LNG RPT (Rapid Phase Transition)”

0 comments on “Modelling liquid-on-liquid spreading during LNG spills”