What is electrophoresis?
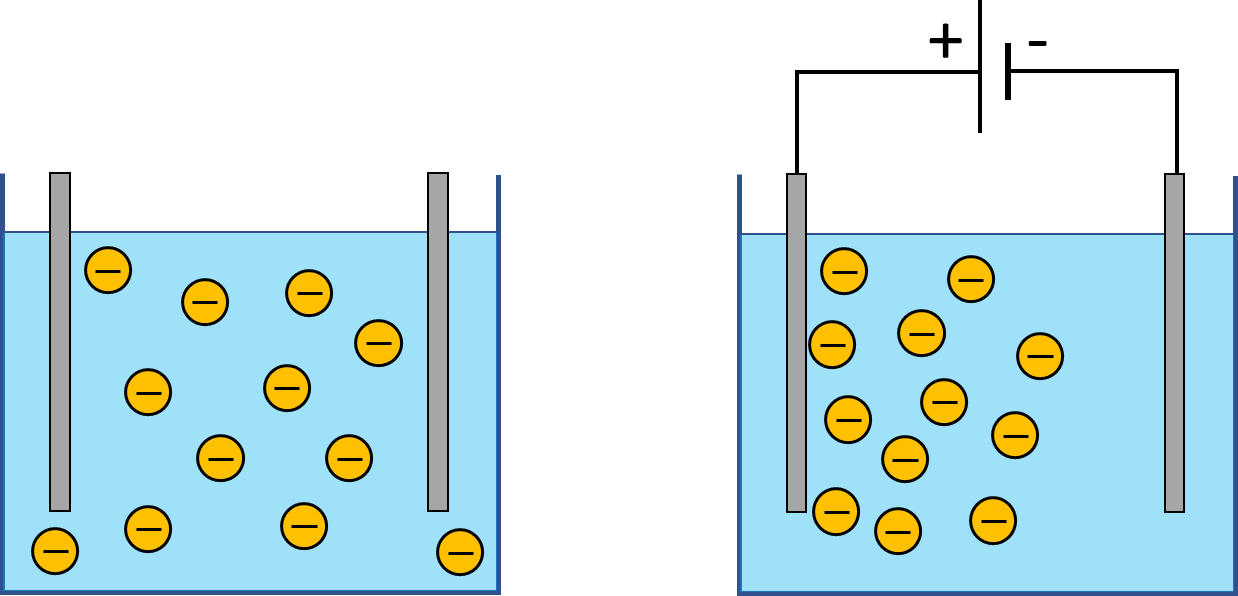
Many fluids found in nature and used in the industry are suspensions of tiny particles in a liquid phase. Often these particles carry electric charge. For instance, clay particles present in drilling fluids usually carry negative charge. This charge appears e.g. when ions in clay minerals are substituted with ions present in the carrier fluid. Similarly, cement particles often carry electric charge as well.
If an electric field is applied to such a suspension, charged particles tend to move towards the electrode of the opposite polarity. This effect is known as electrophoresis. Different sorts of particles often have different electrophoretic mobility – they respond differently to the same applied electric field. Therefore, electrophoresis makes it possible to separate particles based on their type. This effect is exploited e.g. in forensic science where it is used to separate DNA molecules.
Many forces are in play!
Electrophoresis is a deceptively simple effect that can be easily observed in a laboratory experiment. Using this effect in practice requires, however, a good grip on its mechanisms. In addition to being moved by the externally applied electric field, particles interact with each other, especially when they come into closer packing during deposition. Particles also experience the action of the viscous forces as they move through the fluid.
As particles get closer to each other (or to a wall), the so-called lubrication force may become significant: viscous fluid needs to be squeezed out of the interparticle gap in order for particles to approach each other. If particles get very close to one another, a direct mechanical contact can be established, and normal and shear contact forces arise. As a result, the motion of a single particle can be described as follows:

r is the position vector of the particle; Ffield, Fd, Fgb, are the external electric force, the viscous drag force, and the sum of gravity and buoyancy forces acting on the particle; mp and ma are the true mass and the added mass of the particle (added mass accounts for the inertia of the displaced fluid); Filub is the lubrication force caused by interaction with particle i; Fiel is the force of electrostatic interaction with particle i; Flub is the lubrication force caused by the interaction with the walls (e.g. the electrode); Fic is the contact force caused by a direct mechanical interaction with particle i. The latter includes shear and normal components.
The above equation is simply the second law of Newton written for a single particle. Thus, studying the behaviour of a suspension of particles under applied electric field boils down to solving the equation of motion for each particle in the system. One way to solve these equations of motion is by using the discrete-element method (DEM).
Discrete-element modelling of electrophoresis
In DEM, particles are modelled explicitly. In the simplest version, particles are represented as spheres. Simulation proceeds in time steps. At each step, the equation of motion is used to update particle acceleration. Therefrom, particle velocities are calculated and the particle positions updated. After velocities and positions have been updated for all particles, forces are calculated again, and the cycle is repeated. This process is continued until the final simulation time is reached.
The video below shows an example of DEM simulation of electrophoresis. Negatively charged particles are moving towards the anode located on the left. One hundred particles participate in this simulation, with the particle radius uniformly distributed between 1 µm and 50 µm.
DEM enables us to take a closer look at what is going on during electrophoresis, and to do so at particle scale (microns – tens of microns). As such, DEM represents a valuable tool that can support laboratory experiments. Like any other modelling tool, it should be supplemented with experimental data in order to validate the model.
Acknowledgement
This work is part of the project “Voltage on casing for improved well cement quality” (267651/E20) funded by the Research Council of Norway through the PETROMAKS2 program.

0 comments on “Better understanding of electrophoresis through discrete-element modelling”