Industrial processes consume energy when converting raw materials to products. Reducing energy consumption is important to reduce the environmental footprint of the industrial process while improving the profitability. Energy consumption is in the form of electricity and heating/cooling utilities such as steam and cooling water.
The heating and cooling utilities are required to cool hot streams that need to lower their temperature and heat the cold streams that need to increase the temperature as part of the process. At the most basic level, all cooling and heating for process streams can be provided using suitable cold and hot utilities respectively.
In this scenario, the process will use the maximum possible hot and cold utility – leading to a low efficiency and unnecessary cost. It should be possible, where thermodynamically feasible, to heat cold process streams using the hot process streams and vice-versa to lower the use of these utilities.
Pinch analysis and heat integration
Pinch Analysis is a well established thermodynamic approach to minimise hot and cold utility usage in the process by maximising such heat recovery between the hot and cold process streams. This heat recovery between process streams is called heat integration. Given a set of hot and cold process streams with defined starting and ending temperatures, Pinch Analysis allows setting targets for the lowest amount of hot and cold utility requirement and provides a procedure to design the corresponding heat exchanger network.
Learn more about HighEFF
Join our newsletter to stay updated with all the latest research results and news from the HighEFF Research Centre.
This works very well for existing processes where all conditions are fixed. What if the industrial process is being designed from scratch and requires to be optimised? In that case the process conditions of the different streams are not fixed but varying as part of the optimisation/design procedure. The Pinch Analysis targeting procedure does not work as the starting and ending temperatures, as well as the flowrates of the streams are not known. Thus it is not possible to identify optimal heat integration in such cases.
Old work that’s relevant today
Duran and Grossmann published their seminal work, in 1986, on optimising a process along with heat integration. They used the insights of Pinch Analysis and developed a mathematical formulation to minimise hot and cold energy usage in situations where the stream temperatures in the “background” process are not fixed. Their work has been used extensively to simultaneously optimise a process along with heat integration.
It is particularly relevant now with a whole range on new processes being developed related to bioprocessing, novel hydrogen production processes and integration of CO2 capture in industry.
While the Duran-Grossmann model proved to be a powerful way to approach the simultaneous process and heat integration problem, solving it poses numerical challenges. Interest has increased in the Process System Engineering (PSE) field to find ways to reformulate the model due to its high relevance in process design. Four such reformulations have been presented in the literature – (A) smooth approximation, (B) explicit disjunction (C) direct disjunction and (D) intermediate temperature.
The last formulation, intermediate temperature, was the result of collaboration between SINTEF Energy and NTNU. In this reformulation physical insights were used to develop the model rather than pure mathematical considerations and a tighter model with fewer binary variables was developed.
Work and Heat Exchange Networks
While each of the five formulations have their specific advantages, the question that arises from an application perspective is which of these formulations should be used? That is the question we were trying to answer in a paper published last year. The application we considered was Work and Heat Exchange Networks.
Work and Heat Exchange Networks relates to how to design compression and expansion processes. Distinct parts of an industrial process typically operate at different pressures that require process streams to be compressed or expanded. Compression is typically done with electrically driven turbo compressors while turbo expanders drive electric generators to produce electricity.
Thus the goal of Work Exchange Networks is to design processes that consume the least electricity for compression while generating the maximum electricity from expansion. But how does this relate to heat integration?
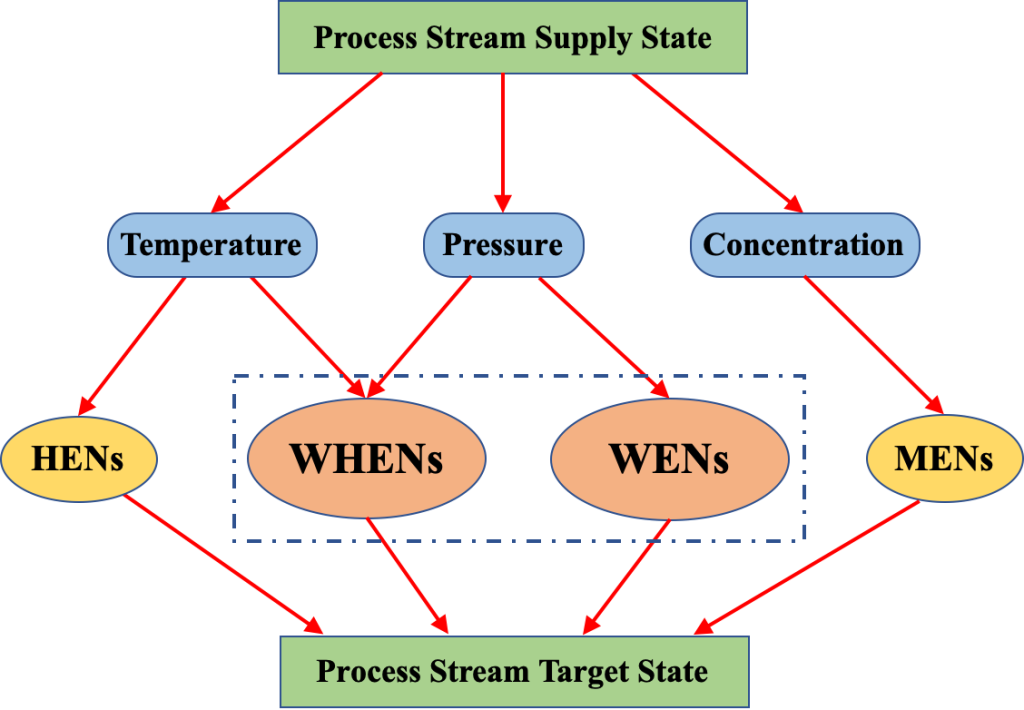
When a stream is compressed, not only does its pressure increase, there is also an associated increase in temperature, while for an expansion process it is the other way around where both pressure and temperature of a process are decreased. Thus it is possible to provide cooling requirement to a process by cooling produced by the expansion process.
This is indeed a standard in refrigeration processes used in the industry and in your refrigerator at home. Hence it is not possible to fix temperature for heat integration when dealing with processes with compressors and expanders that require optimisation. Thus simultaneous process and heat integration is required here.
Our work showed that for small sized problems, the smooth approximation reformulation worked best. The reformulations of the Duran-Grossmann model can only deal with small to moderate scale problems. Since there is a large number of binary variables in the model, it is quite computationally expensive for large-scale problems with the four reformulations evaluated in this study.
In the future, other reformulations or decomposition algorithms should be developed for the Duran-Grossmann model in order to solve complex work and heat exchange network problems.
Learn more about HighEFF
Join our newsletter to stay updated with all the latest research results and news from the HighEFF Research Centre.
This article was written in conjunction with Professor Truls Gundersen, NTNU, and the HighEFF research centre.











Comments
No comments yet. Be the first to comment!