
Deep learning is a branch of artificial intelligence (AI) that is widely used with great success in various fields. However, it has been challenging to apply it to industrial and safety-critical applications due to the lack of guarantees in deep learning models. By combining physics and deep learning in hybrid machine learning we can overcome this barrier. Using Hamiltonian neural networks (HNNs) we bring together the flexibility of deep learning and the security and guarantees from a physics-based modeling approach.
The problem of over-training in deep learning
Deep learning is one of the leading methods within AI due to its flexibility and efficient ways for optimization. Deep neural networks have been shown to be general function approximators, meaning that neural networks can in theory learn anything.
While this sounds great at the beginning, there are two conditions for this statement:
First, you need an infinitely large neural network, and second, infinite amount of data to optimize the network (which might take infinite time) – requirements that are never met in a real application. In the real world, you deal with finite neural networks and finite and noisy data sets, which leads to a problem called over-training. If we use a neural network that is too flexible on a small amount of data, it will learn the specific data set, but not the general structure of the data.
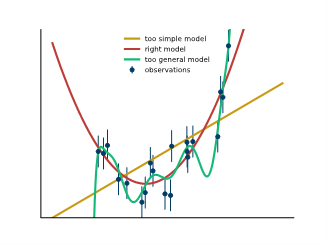
This is illustrated in a way simpler setup in figure 1: The observations are drawn from a simple quadratic function and some noise is added to each data point. We used three simple models: a linear model which is too simple, a quadratic model corresponding to the data distribution, and the green model, which is very flexible and is supposed to represent our neural network. While the simple linear model fails to explain the data, the green model does a better job in explaining the data than the quadratic model, due to the noise and finite data points. But the model has a strange behavior between the data points and these oscillations do not represent our desired behaviour, especially if we know that the true model is quadratic.
Choosing the right model for a physics problem
In the simple example, we could restrict our model to be quadratic, and avoid the problem of over-fitting. The idea behind modelling physical systems with deep learning is the same: Restricting the model to physical behaviour. The classical approach to this is to build a model from first principles of physics and optimize its parameters to observed data. Resulting models have the desired physical behaviour, but they are simplifications of the real-world problem: Anything not included in the physical model cannot be described. Take for example a mechanical problem with friction: Friction can only be modelled approximately because you would need all detail information about the involved surfaces.
Therefore, our goal is to combine the flexibility of deep neural networks with the strictness of the laws of physics. This is especially the case for industrial and safety-critical applications where guarantees of the model behaviour are required but combined with the flexibility of neural networks.
Hamiltonian neural network
So, we want to constrain a neural network to behave according to the laws of physics, but without reducing the flexibility of it. How is that even possible?

The idea behind Hamiltonian neural networks (HNNs) is not to restrict the neural network, but to use it as an element in a larger structure. Thus, the structure will then enforce physics in the system. In a HNN, a neural network is used to learn the Hamiltonian function. The dynamics of the system is then given by the equations of motion (see box on Hamiltonian mechanics). By this, it is guaranteed that energy is always preserved, but with the flexibility of a neural network to approximate very complicated Hamiltonian functions.
Similarly, you can also use HNNs to preserve other quantities like total momentum of the system. Hamiltonian systems are well studied in physics and mathematics and come with guaranteed behaviour, which makes them highly relevant for industrial and safety-critical applications. Of course, Hamiltonian systems are not restricted to mechanics, although this is typically the textbook example; Hamiltonian neural networks can be used in hydrodynamical, electrical or even quantum systems.
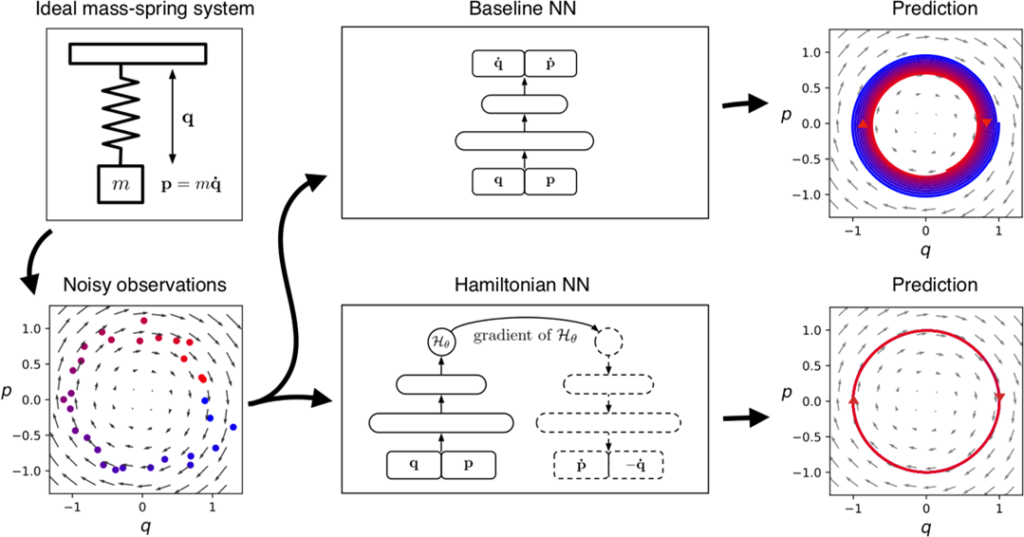
Limitations and extensions of Hamiltonian neural networks
Despite their general setup, HNNs do have limitations: They are mainly developed to study closed systems. In industrial applications, we are interested in open systems with control, where material and energy are entering and leaving, such as a hydraulic system, a furnace, or an electric power grid.
An extension of HNNs are port-Hamiltonian neural networks (PHNNs) [2], following the port-Hamiltonian framework. PHNNs have the same underlying principle as HNNs, but introduce the concept of ports, which allow for external interactions and control. PHNNs are also easily scalable and allow to introduce partial knowledge about the modelled system, which then reduces data requirements when learning the system from data.
The Analytics and AI group at SINTEF is actively researching PHNNs for industrial applications and scalability.
References:
[1] S. Greydanus, M. Dzamba, and J. Yosinski, “Hamiltonian Neural Networks,” arXiv:1906.01563 [cs], Sep. 2019, Accessed: May 06, 2021. [Online]. Available: http://arxiv.org/abs/1906.01563
[2] S. A. Desai, M. Mattheakis, D. Sondak, P. Protopapas, and S. J. Roberts, “Port-Hamiltonian neural networks for learning explicit time-dependent dynamical systems,” Phys. Rev. E, vol. 104, no. 3, p. 034312, Sep. 2021, doi: 10.1103/PhysRevE.104.034312.

0 comments on “New approach for deep learning in safety-critical applications and physical systems”